√100以上 一次関数 問題 応用 211766-一次関数 問題 応��

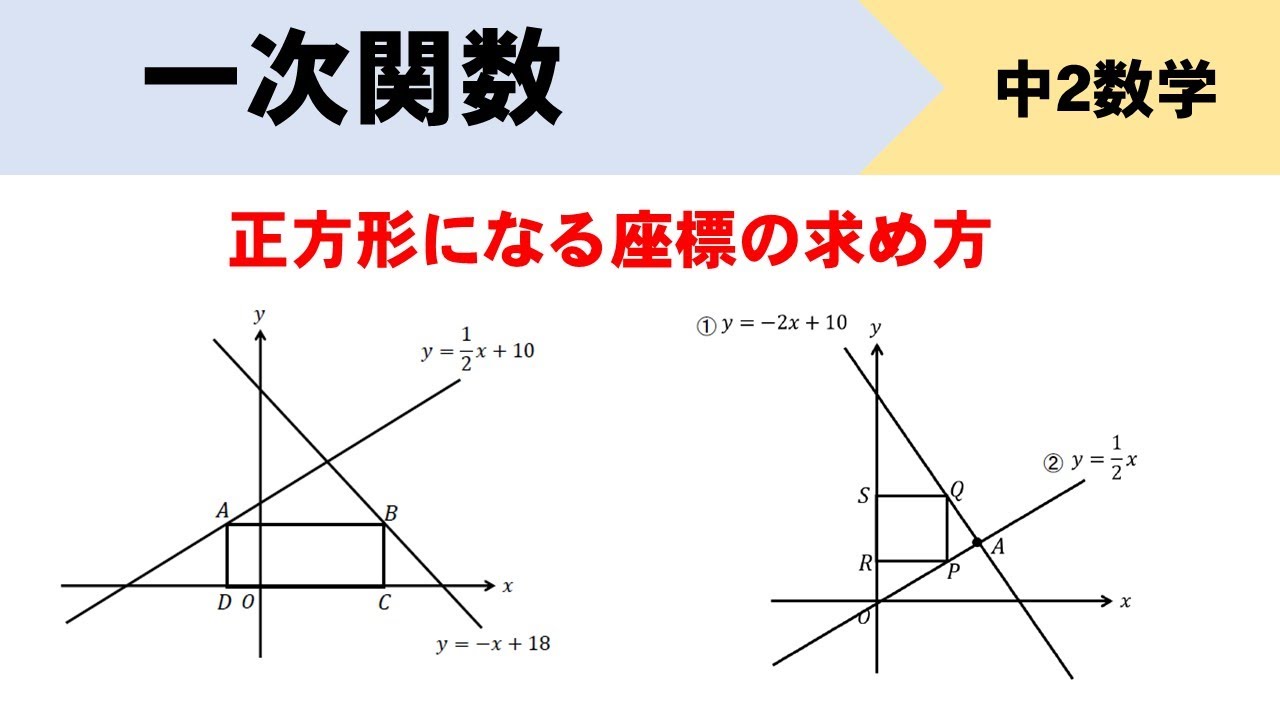
一次関数 正方形になる座標の求め方をイチから 数スタ

第3章 一次関数 アイさんは家から図書館までの道のり4500mを、自転車で毎分300mの速さで進みます。 家を出発してから x 分後の図書館までの残りの道のりを y mとするとき、以下の質問に答え一次関数1 一次関数の式 / 変化の割合 No．1 No．2 No．3 8 一次関数2 一次関数のグラフのかきかた No．1 No．2 No．3 9 一次関数3 一次関数の式の決定 No．1 No．2 No．3 10 一次関数4

一次関数 問題 応用

√99以上 分数の比の求め方 340468-分数の比の求め方

比と比の値についての自主学習ノート例 家庭学習レシピ

 4 回答 分数の比を簡単にする仕方を教えてください。 ☆分数の比を簡単にする →分母の最小公倍数をかける。 1/4 (4分の1)1/3＝ ×12↓ ↓×12 3 です。 なんで1/4が3になるのかも理 今回は、比の値の求め方について書いていきたいと思います。 比の値とは？ 比の値を求める問題 問題① 問題② 問題③ 比の値とは？ a：bという比があったとき、前項aを後項bで割っ

分数の比の求め方

台形の面積の求め方 小学生 280503-台形の面積の求め方 小学生

台形の面積を求める公式は 台形の面積 上底 下底 高さ 台 形 の 面 積 = ( 上 底 下 底) × 高 さ ÷ 2 なので、 台形の面積 台 形 の 面 積 = ( 5 7) × 4 ÷ 2 = 12 × 4 ÷ 2 = 24 ( c m 2) になります。 次は小数点を含む台形の面積を計算します。

画像をダウンロード 三平方 計算 324629

每平方英尺计算btu的3种方法 百科全书 21

 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方三平方の定理とは？ 三平方の定理とは、古代ギリシアの数学者である「ピタゴラス」の名前を取って、「ピタゴラスの定理」と呼ぶこともある定理で、「直角三角形の3辺の長さの関係」表す定理です。 直角三角形とは、中学数学で散々見てきた これですね。

三平方 計算

円柱 表面積 求め方 203163

π × ( r1 r2 )× √ ( ( r1 r2 ) × ( r1 r2 ) 高さ × 高さ ) π × ( r1 × r1 r2 × r2 ) で求めることができます。 底面半径 (r1) ： 上面半径 (r2) ： 高さ (h) ： 表面積 ： 円錐台の体積 円錐台の表面積 円錐台の側面積 使用しているスクリプトの特性から、特に円柱の表面積 ⇒ 2πrh2πr^2 円柱の表面積は、円柱を展開したときの底面積、側面積の合計です。円柱を展開すると「円が2つ」あります。よって底面積は2倍してください。円柱の表面積の求め方は下記が参考になります。 円柱の表面積は？ 体積・表面積の公式や求め方、単位あり計算問題 21年2月19日 この記事では、「円柱」の公式（体積・表面積）や実際の求め方をできるだけわかりやすく解説していきます。 また、リットルなどの単位を含む計算問題なども紹介していきますので、この

円柱の表面積は 1分でわかる公式 求め方 計算 側面積 底面積との関係

円柱 表面積 求め方

【印刷可能】 対角線 正方形 面積 290499-正方形 対角線 長さ 面積

 四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。面積 4 の正方形 面積5 の正方形 （ 2 ）下の枠に（1）以外の面積をもつ正方形を3 つかきましょう。（各枠に1 つずつかきます） 面積（ ）の正方形 面積（ ）の正方形 面積（ ）の正方形 （ 3 対角線が垂直に交わっていれば、次のように変形すればいいのでした。 このことを使えば、正方形の面積は出せますね。 \ 6\times 6\times \dfrac{1}{2}=18 \なので、 $18\mathrm{ cm }^2$ と求められます。

今日 塾で正方形の面積を求めるのに 先生がひし形の面積を求め Yahoo 知恵袋

正方形 対角線 長さ 面積

√ 角柱 体積 公式 308459

6角柱 六角柱 対辺 体積計算 公式 求め方 高さ 自動 volume角柱の体積の公式＝底面積×高さ この公式は、中学校でもよく使うので、声を出して覚える練習すると中学の体積の勉強がわかりやすくなります。 練習問題 次の立体の体積を求めましょう 問題① 底面の形は五角形です技角柱や円柱の体積を，公式を用いて求めることができる。 知 角柱や円柱の体積は，底面積×高さにまとめられることを理解する。 関連※比較・検討場面で「考え方の関連付け」を行う場面は と示し，問題を 問 ，課題を 課 ，めあてを め ，考え方を 考

U9762 U7a4d U548c U9ad4 U7a4d U516c U5f0f U5217 U68 Pdf U9762 U7a4d U548c U9ad4 U7a4d U516c U5f0f U5217 U68 1 U4ee5 U4e0b U70ba U5404 U5e38 U8b U5e73 U9762 U5716 U5f62 U7684 U5468 U754c U53ca U9762 U7a4d U4e4b U516c U5f0f U3002 A U4e09 Ud2

角柱 体積 公式